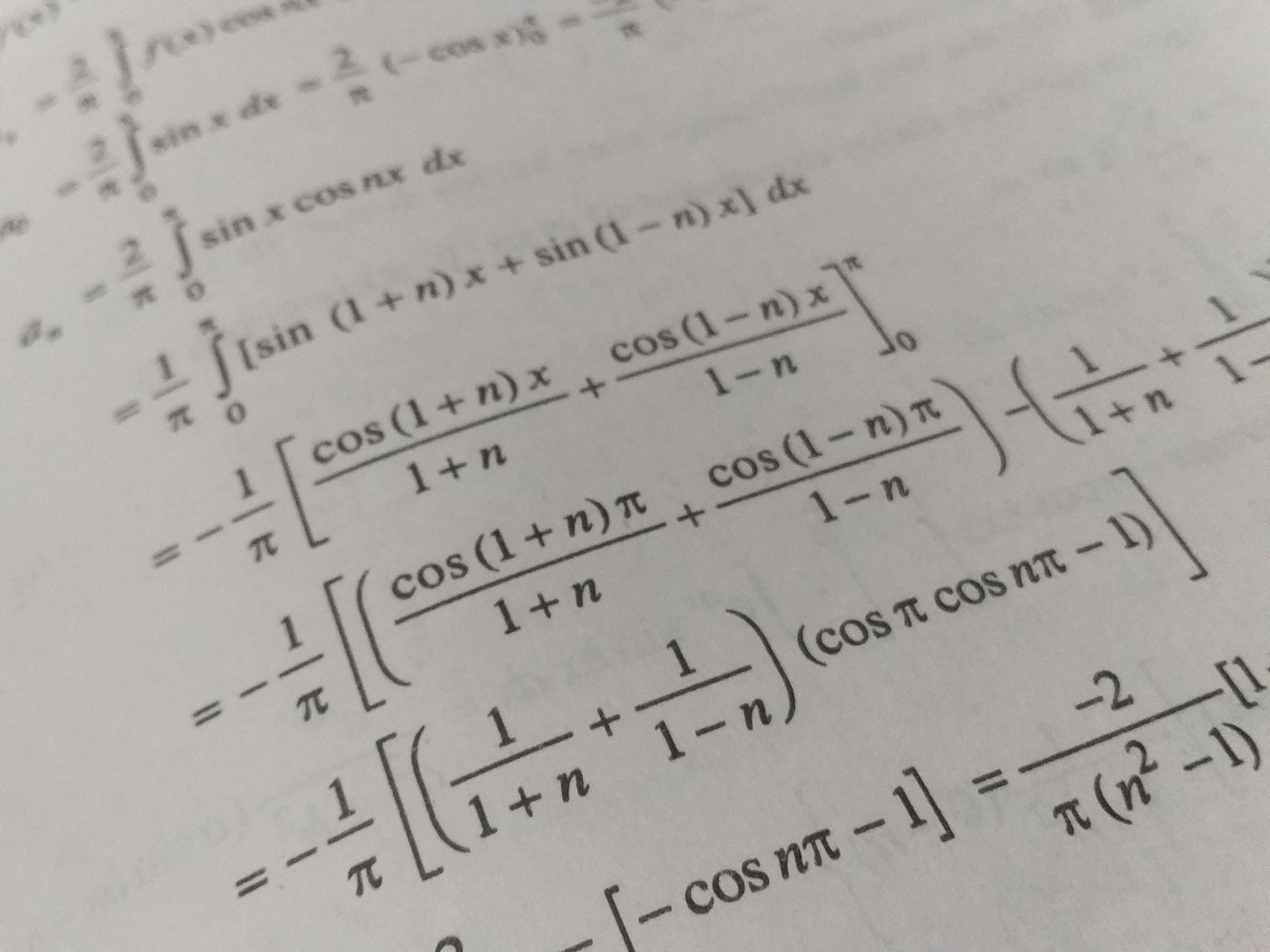
Introduction to Derivatives
In the realm of calculus, derivatives serve as a fundamental component that aids in understanding how functions behave. A derivative measures the rate at which a function changes as its input varies. Essentially, it provides a precise way to quantify how a dependent variable responds to changes in an independent variable. This concept is not only central to mathematics but also extends its significance to fields such as physics, engineering, and economics.
To grasp the essence of derivatives, one must first understand the notion of a function itself. A function describes the relationship between two sets of values, typically an input and an output. When we analyze the behavior of a function at a specific point, the derivative at that point indicates how steep the graph of the function is. In more technical terms, it can be interpreted as the slope of the tangent line that touches the curve of the function at that point.
Derivatives are instrumental in determining various characteristics of functions, such as their maximum and minimum values, concavity, and points of inflection. This analysis is crucial for understanding the general behavior of complex systems. Furthermore, derivatives enable much of the theoretical underpinnings of physics, where they help express quantities like velocity and acceleration through the rate of change of position concerning time.
As we delve deeper into the notion of derivatives, we will uncover not just their theoretical significance but also their practical applications in real-world scenarios. By building a solid foundation in understanding derivatives, we prepare ourselves to explore more advanced topics in calculus, such as integration and the study of trigonometric functions. Derivatives essentially unlock a broader comprehension of how functions operate, setting the stage for a more profound mathematical journey.
The Meaning of Derivatives
Derivatives represent a fundamental concept in calculus, serving as a tool to analyze how a function changes with respect to its variables. At its core, the derivative of a function at a certain point quantifies the rate of change of the function’s output relative to its input, encapsulating the idea of instantaneous change. Geometrically, this can be visualized as the slope of the tangent line at a given point on the graph of the function, providing insights into the behavior of the function in a localized region. When we consider a curve, the derivative allows us to understand how steeply the function rises or falls at any specific point.
Mathematically, if we have a function ( f(x) ), the derivative is denoted as ( f'(x) ) or ( frac{df}{dx} ). This notation reflects the limit of the average rate of change of the function as the interval approaches zero. For example, in physical applications, the derivative can represent the speed of an object when analyzing its position over time. If the function describes position, its derivative provides velocity, indicating how fast the position changes at each instant.
Derivatives prove invaluable across various fields beyond mathematics. In economics, for instance, derivatives help in understanding marginal analysis, where one can assess how changes in production or price affect revenue and cost. This application is crucial in determining optimal solutions for maximizing profit or minimizing cost. Likewise, in physics, derivatives play a vital role in defining concepts like acceleration, which is the derivative of velocity. Through these interpretations, derivatives are shown to be not only mathematical constructs but practical tools essential for solving real-world problems.
Derivatives of Basic Functions
Understanding the derivatives of basic functions is fundamental for mastering more advanced calculus concepts. In this section, we will discuss the derivatives of polynomial functions, exponential functions, and logarithmic functions—each representing a cornerstone in the calculus landscape.
Starting with polynomial functions, the derivative is calculated using the power rule, which states that the derivative of ( ax^n ) is ( nax^{n-1} ). For instance, if we take the polynomial function ( f(x) = 3x^3 + 5x^2 – 4x + 7 ), its derivative ( f'(x) ) is computed as follows: \( f'(x) = 3 cdot 3x^{3-1} + 2 cdot 5x^{2-1} – 4 \) simplifying to ( f'(x) = 9x^2 + 10x – 4 ).
Next, we consider exponential functions, expressed in the form ( f(x) = a^x ) where ( a ) is a constant. The derivative of such a function is given by the formula ( f'(x) = a^x ln(a) ). For example, if we have ( f(x) = 2^x ), the derivative would be ( f'(x) = 2^x ln(2) ). This characteristic is particularly useful in various applications, including growth models.
Logarithmic functions provide another essential area for derivative computation. For a function represented as ( f(x) = ln(x) ), the derivative can be succinctly expressed as ( f'(x) = frac{1}{x} ). This is particularly useful when dealing with integration and other aspects of calculus. For example, the derivative of ( f(x) = ln(3x) ) would use the chain rule, giving: ( f'(x) = frac{3}{3x} = frac{1}{x} ).
In conclusion, grasping the derivatives of these basic functions lays a solid foundation for exploring more intricate mathematical concepts, such as trigonometric functions, in subsequent sections of this guide.
Derivatives of Trigonometric Functions
The derivatives of trigonometric functions play a critical role in calculus, particularly when analyzing the behavior of periodic functions. The foundational derivatives include those of the sine, cosine, and tangent functions. Each of these functions has unique properties that contribute to their differentiation.
The derivative of the sine function, denoted as sin(x), is given by the formula d/dx [sin(x)] = cos(x). This relationship illustrates that the rate of change of sine is equal to the cosine function. The geometric interpretation of this derivative can be visualized on the unit circle, where cosine represents the horizontal coordinate of the point corresponding to the angle x.
Similarly, the cosine function has a derivative expressed as d/dx [cos(x)] = -sin(x). The negative sign indicates that as the angle increases, the cosine value decreases, and vice versa. This relationship is equally important when tackling problems related to motion and oscillation.
The tangent function, defined as tan(x) = sin(x)/cos(x), has a derivative given by d/dx [tan(x)] = sec²(x). This result is particularly useful for solving differential equations where the tangent function is involved. Additionally, the secant function, sec(x) = 1/cos(x), forms a significant part of many calculus applications.
For example, if we want to differentiate f(x) = tan(2x), we apply the chain rule: f'(x) = 2sec²(2x). This showcases how the derivative of trigonometric functions can be combined with other calculus principles for more complex expressions.
In summary, understanding the derivatives of trigonometric functions such as sine, cosine, and tangent is crucial for applications in physics, engineering, and beyond. Mastery of these derivatives allows for deeper insights into various mathematical models and real-world phenomena.
Applying Derivatives to Trigonometric Functions
Derivatives are essential tools in calculus that enable the analysis of the behavior of functions, particularly trigonometric functions. When applying derivatives to trigonometric functions, we can ascertain critical values such as maxima, minima, and points of inflection. To achieve this, we often start by finding the derivative of the trigonometric function in question.
For instance, consider the sine function, represented as (f(x) = sin(x)). The derivative of the sine function is given by (f'(x) = cos(x)). To find the local maxima or minima, we set the derivative equal to zero, leading to the equation (cos(x) = 0). Solving this equation reveals that local maxima occur at odd multiples of (frac{pi}{2}), while local minima occur at even multiples of (frac{pi}{2}). This technique can also be applied to the cosine function, where the analysis will reveal similar critical points using (f'(x) = -sin(x)).
Moreover, identifying points of inflection requires us to evaluate the second derivative of the function. For (f(x) = sin(x)), the second derivative is (f”(x) = -cos(x)). Setting this equal to zero allows us to assess the concavity of the function, revealing where it changes from concave upward to concave downward, and vice versa.
In practical applications, employing these derivative concepts can lead to enhanced understanding of trigonometric models, particularly in fields such as physics and engineering where oscillatory motion is involved. Whether optimizing a wave function or analyzing periodic phenomena, using derivatives effectively provides valuable insight into critical behavior of trigonometric functions. By mastering these derivative applications, one can better tackle complex problems involving trigonometric variations and their implications in real-world contexts.
Derivatives of Inverse Trigonometric Functions
The study of derivatives associated with inverse trigonometric functions, such as arcsin, arccos, and arctan, is crucial in calculus and various applications. These functions are the inverse operations of the basic trigonometric functions, which leads to unique derivatives that serve various mathematical purposes. Understanding these derivatives not only aids in calculus but also provides insights into areas like physics, engineering, and other mathematical domains.
To derive the formulas, let’s first consider the function y = arcsin(x). By differentiating both sides implicitly, we get sin(y) = x. Following the chain rule, we derive that cos(y) dy/dx = 1. Since cos(y) can also be expressed using the Pythagorean identity as √(1 – x²), the derivative thus simplifies to dy/dx = 1/√(1 – x²) for -1 < x < 1. This foundational derivative is frequently utilized when dealing with integrals involving arcsin.
Similarly, for the function y = arccos(x), we start with cos(y) = x. Applying implicit differentiation results in -sin(y) dy/dx = 1. Hence, dy/dx resolves to -1/√(1 – x²), valid for the same interval. Both arcsin and arccos derivatives share a remarkable resemblance but differ only by a negative sign, which reflects the nature of their inversions.
The final function, arctan(x), follows a comparable process. Setting y = arctan(x) gives tan(y) = x. Differentiating implicitly yields sec²(y) dy/dx = 1. Utilizing the identity sec²(y) = 1 + tan²(y), we find dy/dx = 1/(1 + x²). This functional form is pivotal in many calculus problems, especially involving integration techniques.
In general, the derivatives of inverse trigonometric functions are essential in various mathematical fields, helping to solve complex problems and making them increasingly relevant in applied scenarios. Mastery of these derivatives can lead to more profound insights and applications in advanced mathematics.
Applications of Inverse Trigonometric Derivatives
The derivatives of inverse trigonometric functions play an essential role in various practical applications across different fields, including engineering, physics, and even economics. These derivatives, stemming from foundational principles of calculus, offer invaluable tools for solving complex problems where angles and ratios are involved.
One significant application of inverse trigonometric derivatives can be observed in engineering, particularly in analyzing mechanical systems. For instance, when dealing with the design of bridges or roads, engineers often need to consider angles of elevation and depression. The derivative of the inverse tangent function, which expresses the angle as a function of horizontal and vertical distances, is crucial for calculating the right angles necessary for safe construction. By applying such derivatives, engineers can ensure that structures support prescribed loads and resist forces applied at various angles.
Furthermore, the field of physics extensively utilizes inverse trigonometric derivatives, especially in wave mechanics and optics. For example, when analyzing the trajectories of projectiles or light rays, physicists may use the inverse sine function to determine the angle at which the projectile is launched, considering its initial velocity and height. By differentiating the inverse sine function, they find how these angles change with respect to time or distance, enabling them to predict the behavior of various physical systems accurately.
Additionally, inverse trigonometric derivatives find utility in economics, particularly in modeling various phenomena involving cyclical behavior. Economists may employ the derivatives of inverse trigonometric functions to analyze trends and fluctuations in markets, allowing for more informed decision-making regarding investments and resource allocation. By understanding the rate of change in these angles, analysts can gauge the volatility and stability of economic indicators effectively.
In conclusion, the derivatives of inverse trigonometric functions are instrumental across various disciplines, allowing professionals to tackle real-world problems through precise calculations of angles. Their applications span engineering, physics, and economics, highlighting the significance of these mathematical tools in practical scenarios.
Common Mistakes and Misunderstandings
When students first encounter derivatives, particularly of trigonometric and inverse trigonometric functions, they often fall into several common pitfalls. One prevalent mistake is neglecting to apply the chain rule correctly when dealing with composite functions. For instance, when differentiating a function like sin(f(x)), students sometimes forget to multiply by the derivative of the inner function, f(x). This oversight can lead to incorrect results and a lack of understanding of how nested functions interact during differentiation.
Another frequent misunderstanding arises from the properties of inverse trigonometric functions, specifically their ranges. For example, while the derivative of arcsin(x) is 1/√(1-x²), some students mistakenly assume that the derivative of all functions involving arcsin will yield similar expressions without careful consideration of their domain and range. Recognizing the constraints on these functions is essential not only for performing accurate differentiation but also for understanding the behavior of these functions on specified intervals.
Additionally, confusion may occur when differentiating trigonometric functions, especially regarding the negative signs that appear. For instance, when working with cos(x), students should be cautious to note that the derivative is -sin(x). Failing to remember these fundamental properties can lead to incorrect evaluations and hinder comprehension of related problems.
To avoid these errors, students can benefit from practicing differentiation through a variety of exercises and examples that emphasize both direct and inverse trigonometric functions. Furthermore, creating a comprehensive checklist of fundamental differentiation rules, including recognizing when to apply the product or quotient rule, can significantly aid in minimizing mistakes. Reinforcement of conceptual understanding of function behavior can provide clarity, ultimately leading to a more solid grasp of derivatives and their applications.
Conclusion and Further Reading
In this comprehensive guide to derivatives, we have explored the essentials of trigonometric functions and their applications in calculus. We delved into the fundamental concepts of derivatives, including definitions, notations, and the significance of limits. The discussion also covered the specific derivatives of key trigonometric functions, namely sine, cosine, tangent, and their co-functions, providing formulas that are crucial for further mathematical analysis.
The trigonometric derivatives not only serve as foundational tools for solving problems in calculus but also play an integral role in various fields, including physics, engineering, and computer science. Understanding how to differentiate these functions equips students and professionals alike with the skills necessary to analyze oscillatory behaviors and waveforms, among other applications. Moreover, the interrelations among these functions deepen our comprehension of their geometric interpretations and real-world implications.
To reinforce your understanding of derivatives, it is advisable to engage with additional resources. Textbooks such as “Calculus: Early Transcendentals” by James Stewart provide detailed explanations and practice problems, while online platforms like Khan Academy and Coursera offer interactive lessons and exercises. Furthermore, exploring advanced topics such as implicit differentiation and partial derivatives can enhance your mathematical toolkit. Engaging with practice problems not only solidifies your skills but also prepares you for more complex problems that you might encounter in higher-level studies.
In conclusion, a strong grasp of derivatives, particularly in the context of trigonometric functions, is indispensable in mathematics. Continuing to explore this topic through additional readings and exercises will undoubtedly bolster your ability to apply these concepts successfully.