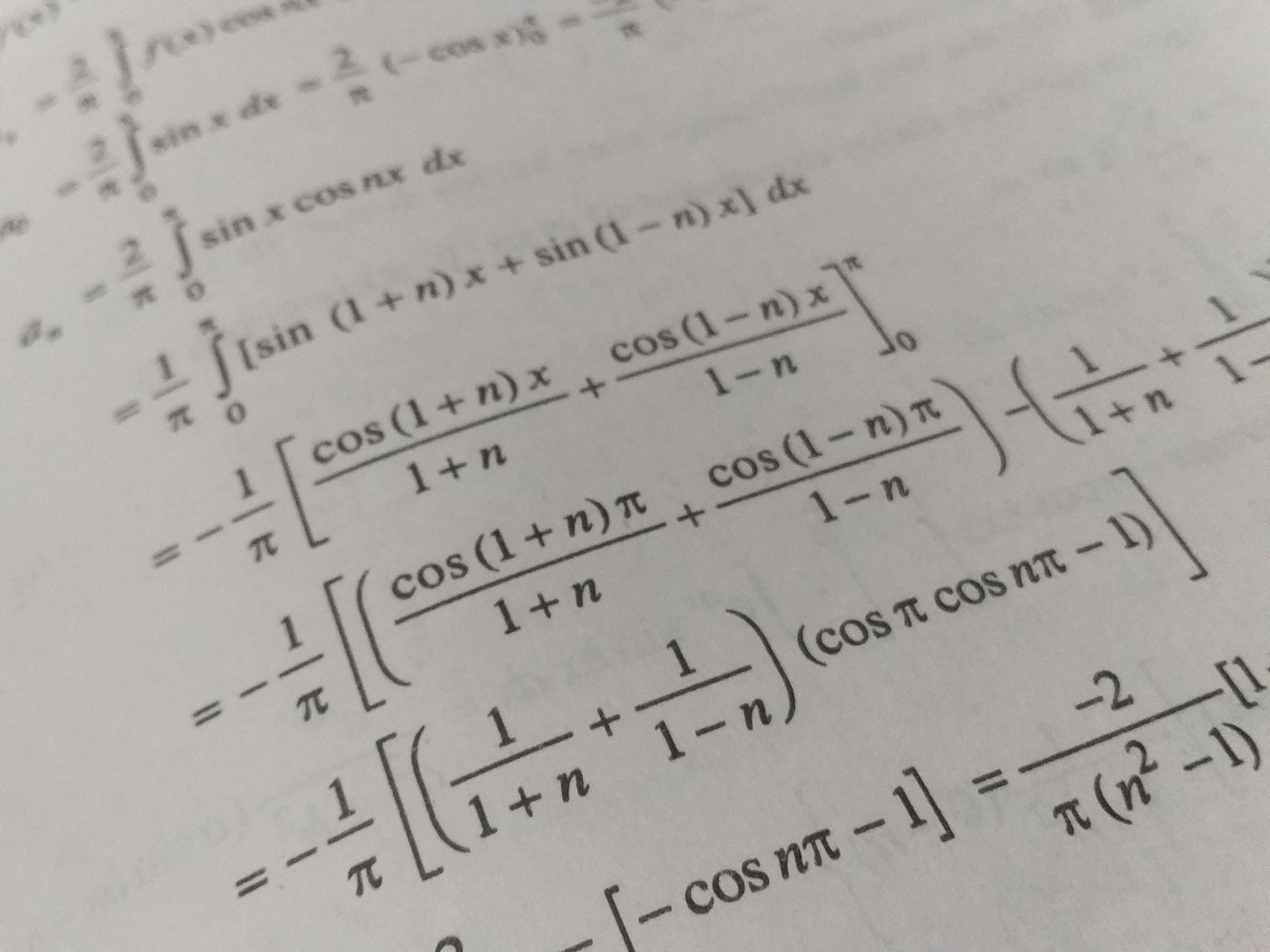
What are Derivatives?
Derivatives are a fundamental concept in calculus, representing the instantaneous rate of change of a function with respect to its variable. Specifically, if ( f(x) ) is a function, the derivative, denoted as ( f'(x) ) or ( frac{df}{dx} ), quantifies how ( f(x) ) changes as ( x ) changes. This concept is pivotal in various fields of mathematics, physics, engineering, and economics, as it provides essential insights into the behavior of functions.
The significance of derivatives can be observed in numerous applications. For instance, in physics, the derivative of an object’s position with respect to time yields its velocity, a crucial measure of motion. Similarly, the second derivative can indicate acceleration, illustrating how the velocity of an object changes over time. In mathematics, derivatives help analyze the behavior of functions, permitting the identification of critical points, such as maxima, minima, and points of inflection, which are vital for understanding function graphs.
Furthermore, derivatives find extensive use in engineering, where they aid in modeling dynamic systems, ensuring safety and efficiency in designs. In economics, derivatives are employed in calculating marginal cost and revenue, enabling businesses and economists to make informed decisions based on changing economic conditions. By examining derivatives, one can also predict trends and optimize various processes, reflecting their crucial role in strategic planning.
In summary, derivatives provide a powerful tool for understanding and analyzing the behavior of functions. They encapsulate the concept of change, enabling the exploration of various phenomena in real-world applications. The study of derivatives is, therefore, essential for anyone seeking to grasp the intricacies of calculus and its implications across multiple disciplines.
Derivatives of Trigonometric Functions
The derivatives of trigonometric functions are integral to various fields, including calculus and engineering. Understanding these derivatives is essential for solving complex problems involving motion, waves, and oscillations. There are six fundamental trigonometric functions, each with specific derivatives: sine, cosine, tangent, cosecant, secant, and cotangent.
The derivative of the sine function, denoted as sin(x), is cos(x). This relationship is crucial as it highlights how the rate of change of the sine function corresponds directly to the cosine function. Conversely, the derivative of the cosine function, cos(x), is -sin(x). This negative sign indicates that the cosine function decreases when the sine function increases, representing a fundamental aspect of trigonometric relationships in periodic functions.
Moving on to the tangent function, which is represented as tan(x), its derivative is sec²(x). The secant function sec(x) has a derivative of sec(x)tan(x), while the cosecant function csc(x) yields a derivative of -csc(x)cot(x). Finally, the derivative of the cotangent function cot(x) is -csc²(x).
Graphically, these relationships can be illustrated through the unit circle or through tangent lines to the curves of each function. For instance, at any point on the sine wave, the slope of the tangent line is represented by the cosine value at that point. Similarly, the derivative’s graphical representation for the tangent function is steepest at points approaching asymptotes, where the behavior of these derivatives illuminates profound relationships between angles and their rates of change.
These derivatives are pivotal in various applications, including physics problems that deal with angular motion and even in financial calculus, where periodic functions are frequently analyzed. Understanding the derivatives of trigonometric functions thus not only enhances mathematical proficiency but also equips students with the tools to tackle real-world problems effectively.
Understanding Inverse Trigonometric Functions and Their Derivatives
Inverse trigonometric functions play a crucial role in calculus, particularly when it comes to understanding their derivatives. The three primary inverse trigonometric functions are arcsine (sin-1), arccosine (cos-1), and arctangent (tan-1). Each of these functions provides a way to determine the angle corresponding to a given trigonometric ratio. This relationship between the standard trigonometric functions and their inverses is fundamental when calculating the derivatives of these functions.
The derivative of the arcsine function is given by the formula: (d/dx) arcsin(x) = 1/√(1-x²), valid for the interval -1 < x < 1. The arccosine function, alternatively, has its derivative expressed as (d/dx) arccos(x) = -1/√(1-x²). Notably, the negative sign indicates that the arccosine function is a decreasing function. In contrast, the derivative of the arctangent function is (d/dx) arctan(x) = 1/(1+x²). This positive derivative reflects that the arctangent function is always increasing.
Students often experience confusion surrounding the signs of the derivatives, especially when considering the ranges and behavior of these functions. For instance, arcsine and arctangent are defined across all real numbers, whereas arccosine is restricted to the interval [0, π]. Therefore, while working on problems involving limits and derivatives, it is essential to understand these constraints to avoid common pitfalls.
For practical application, consider the function y = arcsin(x). To find its derivative at a specific point, such as x = 0.5, substitute 0.5 into the derivative formula, yielding a precise result vital for solving calculus problems. Recognizing the importance of these derivatives is critical for mastering calculus concepts and effectively applying them in various mathematical contexts.
Applications of Derivatives in Real Life
The concept of derivatives extends beyond the confines of mathematics, finding applications across various fields such as physics, engineering, and economics. In physics, derivatives are indispensable in analyzing motion. The derivative of position with respect to time results in velocity, which reflects the rate of change of position. Similarly, the derivative of velocity results in acceleration, indicating how quickly an object is speeding up or slowing down. For instance, in kinematics, understanding the derivative of the displacement function allows physicists to predict the future position of objects in motion, a critical aspect in fields such as mechanics and robotics.
In engineering, derivatives play a pivotal role in design and optimization problems. Engineers utilize derivatives to determine the steepest ascent or descent in various scenarios, such as optimizing the materials and structures to achieve the safest and most cost-effective designs. A practical example is in civil engineering, where derivatives help in assessing load distributions and stress-strain relationships in infrastructures like bridges and buildings. By applying the principles of calculus, engineers can calculate the most efficient materials to use, ensuring durability while minimizing costs.
Economics also heavily relies on derivatives, particularly in understanding cost functions and rates of change. The derivative of a cost function provides insight into marginal costs, which can inform businesses about the additional expense incurred when producing one more unit of a good or service. This understanding aids in pricing strategies and maximizing profits. Moreover, derivatives help in analyzing demand, supply, and the impact of external economic variables, ensuring that businesses can adapt to market changes effectively.
Overall, the applications of derivatives across different disciplines underscore their significance in modern problem-solving. By facilitating a deeper understanding of change and rates, derivatives equip professionals to make informed decisions based on quantitative analysis, thereby enhancing productivity and innovation in various sectors.